1) Escolha o melhor material para estudar matemática
”A maioria das pessoas não planeja fracassar, fracassa por não planejar.”
John L. Beckley
Escolher o melhor material para aprender matemática é algo muito pessoal e depende do seu propósito de estudo e o seu nível de conhecimento. Entretanto, é importante levar em consideração algumas questões.
a) Livro de matemática
Escolha um livro-texto que apresenta bastante exemplos resolvidos e relacionam a teoria com aplicações no dia a dia.
- Se você já tem um conhecimento intermediário:
Escolha um livro-texto mais "enxuto" com a organização por definições, teoremas e corolários. Para os estudantes do ensino médio e que prestarão vestibular e Enem vale a pena conferir a análise que fiz dos livros didáticos sugeridos pelo Ministério da Educação - MEC.
b) Videoaula de matemática
Além da escolha de um bom livro base, assistir videoaulas pode ajudar bastante na compreensão do conteúdo. Já que você poderá assistir e voltar naquela parte que não entendeu direito. Na internet tem muito material bom e gratuito de matemática com excelentes professores. Porém, estão espalhadas e precisa de um bom tempo para encontrar as melhores videoaulas.
2) Organize o local e horário de estudos
”Nós somos o que fazemos repetidas vezes, repetidamente. A excelência portanto não é um feito, mas um hábito.”
Aristóteles
a) Local de estudos
Escolha um lugar da sua casa para ser o seu ambiente de estudos. Leve em consideração que este local deve preferencialmente:
- Ser silencioso, que não possua distrações como televisão, telefone, etc;
- Ter boa iluminação e ventilação;
- Possuir uma mesa de estudos e cadeira confortável;
- Tenha à disposição água, uma fruta ou alimento saudável.
Na impossibilidade dessas condições, considere a opção de estudar na biblioteca ou em sala de estudos.
b) Horário de estudos
Crie um cronograma semanal com todas as suas atividades e em seguida defina o horário mais adequado para você estudar. Crie o hábito de estudar nesse mesmo horário. O hábito tornará mais prazeroso o estudo. Porém, não fique escravo desse cronograma. Caso ocorra alguma coisa que impossibilite de estudar no horário definido, nada impede de estudar em outro horário.
Caso tenha que conciliar o estudo da matemática com outras disciplinas, uma forma que encontrei para otimizar o estudo e aumentar a quantidade de horas estudadas sem se cansar e sem perder a qualidade foi por meio do método de ciclo de estudos que intercala matérias de exatas e humanas usando as várias áreas do cérebro e aumentando a produtividade nos estudos. Vale a pena utilizar essa estratégia para organizar seus estudos.
3) Domine a teoria
"Conheces a Matemática e dominarás o mundo."
Galileu Galilei
"Conheça todas as teorias, domine todas as técnicas, mas ao tocar uma alma humana, seja apenas outra alma humana."
Carl Jung
O que torna a matemática difícil é o fato de ser uma matéria contínua. Ou seja, com pré-requisitos. Exemplo: Para entender a tabuada de multiplicar você precisa saber somar. ( Caso ainda tenha problema com isso aprenda de vez com jogos de tabuada).
Então, para você conseguir avançar em seu estudos, é necessário que você domine as noções básicas. Não tem como fugir. É muito importante conhecer a linguagem matemática e seus símbolos.
Além disso, o entendimento da distribuição dos ramos da matemática trazem uma visão ampla dessa ciência facilitando o seu estudo .
Aprenda as definições matemáticas. Uma definição matemática é uma verdade demonstrada que serve de base para estruturar o raciocínio lógico matemático. Aceite essa verdade e concentre-se na sua aplicação para a resolução dos problemas.
Sempre que aprender uma nova definição e/ ou teorema da matemática tente relacioná-lo com alguma aplicação no dia a dia, lembre- se matemática nada mais é do que uma interpretação da natureza. Esse exercício dará maior consistência para assimilar o assunto.
Crie um formulário de expressões matemáticas para consultas rápidas. Separe uma parte do caderno apenas para fórmulas matemáticas. Assim, quando precisar recordar de alguma ela estará ali a sua disposição. Não se preocupe em memorizar essas fórmulas, isso acontecerá naturalmente conforme você for aplicando- as em exercícios.
Resolva os exercícios resolvidos. Nos livros- textos, costuma- se ter exercícios resolvidos. Tente resolvê-los sem olhar a solução. Se tiver dificuldade, veja a parte que está com dificuldade e volte na resolução até conseguir chegar na conclusão sozinho.
Desta forma, para dominar a teoria temos que:
- Conhecer a linguagem matemática e seus símbolos;
- Aprender as definições matemáticas;
- Relacionar a teoria com alguma aplicação no dia a dia;
- Criar lista de fórmulas e expressões matemáticas;
- Resolver os exercícios resolvidos.
Está gostando deste artigo?
Insira aqui o seu email para receber gratuitamente as atualizações do blog! ( é grátis)
 Respeitamos a sua privacidade e não achamos nada legal spam.
Respeitamos a sua privacidade e não achamos nada legal spam.
4) Pratique exercícios
"Cada problema que resolvi tornou-se uma regra, que serviu depois para resolver outros problemas."
René Descartes
Assim como para se tornar um grande maratonista é necessário muito treino e dedicação. Para ficar bom em matemática é preciso praticar muitos exercícios de matemática. Muito mesmo!
Para resolver problemas matemáticos, primeiramente entenda o enunciado da questão e saiba qual é o seu objetivo. Sempre se pergunte: O que o exercício quer? Não despreze a interpretação de texto. Vejo muitos estudantes que sabem as definições matemáticas mas não conseguem resolver o problema por não entender o que o exercício pede. Não tem como separar, para ser um bom matemático você precisa dominar bem a língua portuguesa e saber interpretar textos.
Uma vez entendido o enunciado do problema, divida o exercício em quantas partes forem necessárias para solucioná-lo e vá resolvendo por partes. Ao final, conecte todas essas partes e chegue na solução. Cuidado para não repartir demais o problema e esquecer qual é o seu real objetivo.
Erre bastaste. quanto mais erros você cometer, mais você aprenderá. A cada erro você tirará uma nova lição e assimilará melhor o conteúdo. Não desanime.Identifique os seus erros e refaça as questões erradas buscando entender em que parte você errou.
Desta forma, para praticar exercícios temos que:
- Entender o enunciado do problema;
- Dividir o exercício em problemas menores;
- Errar e aprender com os erros;
- Utilizar jogos de matemática para assimilar e reter o conteúdo.
5) Tire todas as suas dúvidas
"A dúvida permite extrair um núcleo de certeza, que cresce a medida que ela se radicaliza: É indubitável que, se duvido, penso."
René Descartes
Quando estiver praticando exercícios coloque uma interrogação naqueles problemas que você não conseguiu resolver. Durante a correção de exercícios, tire suas dúvidas e esclareça as questões em que você apresentou dificuldade. Assim que puder, resolva- o novamente entendendo a parte que não tinha ficado clara.
Conclusão
Como disse no início, matemática é a interpretação e representação dos acontecimentos da natureza. E se você domina bem a matemática terá maior facilidade em solucionar os problemas do dia a dia. Daí a importância de conhecer e gostar de matemática.
Para isso, mostrei neste artigo 5 passos para aprender matemática, que são estes:
- Escolha o melhor material para estudar matemática
Organize o local e horário de estudos
Domine a teoria
Pratique exercícios
Tire todas as suas dúvidas
Siga esses passos e tenho certeza que seu desempenho em matemática passará para outro patamar.
Se gostou deste artigo, curta a nossa página no Facebook/ Google+ e compartilhe com os amigos.
Continue acompanhando o blog que teremos mais dicas e postagens de aulas de matemática com videoaulas.
Tenho uma pergunta para você...
Você já aplica esses passos ou algum outro? Ficou com alguma dúvida em algum desses passos?
Deixe o seu comentário. Nos falamos logo abaixo.
Até mais!
Fonte: http://matematicazup.com.br/como-aprender-matematica/
 ,
,  e
e  , determine a matriz D resultante da operação A + B – C.
, determine a matriz D resultante da operação A + B – C.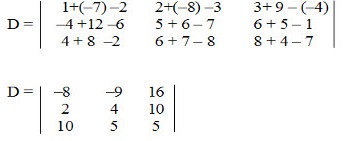


.gif)
.gif)
.gif)