VÍDEO AULA - A Origem dos Números

A CRIAÇÃO DOS NÚMEROS

A CRIAÇÃO DOS NÚMEROS 

Os números foram inventados pelos homens. Mas sua criação não aconteceu de repente surgiu da necessidade de contar coisas. O homem primitivo, por exemplo, contava traçando riscos na madeira ou no osso, ou ainda, fazendo nós em uma corda. Como era difícil contar quantidades grandes e efetuar cálculos com pedras, nós ou riscos simples, a necessidade de efetuar cálculos com maior rapidez levou o homem a criar símbolos, para representar quantidade. Na antiguidade, nem todos os povos usavam os mesmos símbolos. Vamos conhecer como alguns povos dessa época contavam. 

A NUMERAÇÃO DOS ROMANOS

Os romanos representavam quantidades usando as próprias letras de seu alfabeto:

I - valia uma unidade 
V - valia cinco unidades 
X - representava dez unidades 
L - indicava cinqüenta unidades 
C - valia cem unidades 
D - representava quinhentas unidades 
M - indicava mil unidades 

As quantidades eram representadas colocando-se os símbolos uns ao lado dos outros, conforme a seguinte regra: 

Os símbolos iguais juntos, até três , significava soma de valores: 

II = 1 + 1 = 2 

XXX = 10 + 10 + 10 = 30

CCC = 100 + 100 + 100 = 300

Dois símbolos diferentes juntos, com o número menor aparecendo antes do maior, significava subtração de valores:

IV = 5 - 1 = 4 

XL = 50 - 10 = 40 

XC = 100 - 10 = 90

Dois símbolos diferentes juntos, com o maior aparecendo antes do menor, significa soma de valores: 

LX = 50 + 10 = 60 

CCXXX = 200 + 30 = 230 

DC = 500 + 100 = 600 

MMMD = 3000 + 500 = 3500

Para indicar quantidades a partir de 4000, os romanos usavam um traço horizontal sobre as letras correspondentes à quantidade de milhares: 

__ 
IV = 4000 
_ 
V = 5000 
_ 
VCCCXX = 5320
_____ 
XXIII = 23000 

obs: Os Romanos não conheciam um símbolo para representar o número zero. 

A NÚMERAÇÃO DOS HINDUS

Foram os hindus que inventaram os símbolos que usamos até hoje : 0,1,2,3,4,5,6,7,8 e 9 

Esses símbolos, divulgados pelos árabes, são conhecidos como algarismos indo-arábicos e com eles escrevemos todos os números.

Mais adiante vamos falar sobre o sistema de numeração que usamos. Você sabe, por exemplo, que 51 e 15 representam quantidades bem diferentes. 

NÚMEROS NATURAIS


Quando contamos uma quantidade de qualquer coisa (objetos animais, estrelas pessoas etc ) empregamos os números 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15...

Esses números são chamados de números naturais. Existem infinitos números naturais os números que aparecem juntos, como na seqüência acima são chamados números consecutivos. 

Por exemplo 12 e 13 são consecutivos 13 é o sucessor (vem depois ) e 12 é o antecessor (vem antes) de 13.

Observações: 

1) todo número natural tem um sucessor (é o que vem depois) 
2) todo número natural tem um antecessor (é o que vem antes), com exceção do zero. 
3) Um número natural e o seu sucessor são chamados números consecutivos.

PAR OU IMPAR 

Um número natural é par quando termina em 0,2,4,6 ou 8 
Os números pares são: 0,2,4,6,8,10,12,14,16...
Um número é ímpar quando termina em 1,3,5,7, ou 9. 
Os números ímpares são: 1,3,5,7,9,11,13,15...

Bons estudos e até a próxima!

Professora Danielle Cavalcante Soares.

VÍDEO AULA - Matriz

EXERCÍCIOS RESOLVIDOS - Matriz

1) Dadas as matrizes  ,    e   , determine a matriz D resultante da operação A + B – C.

Resolução:

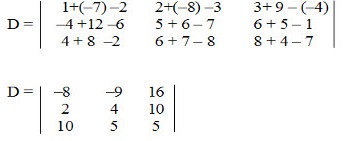
 2) Os elementos de uma matriz M quadrada de ordem 3 x 3 são dados por a_ij, onde:

i + j, se i ≠ j

0, se i = j

Determine M + M.

Resolução:

3) (PUC–SP–Adaptada) São dadas as matrizes A = (aij) e B = (bij), quadradas de ordem 2, com aij = 3i + 4j e bij = – 4i – 3j. Considerando C = A + B, calcule a matriz C.

Resolução:

Bons estudos!

Professora Danielle Cavalcante Soares.

VOCÊ SABIA???

Conheces o Número Mágico?

1089 é conhecido como o Número Mágico. Vê porquê.

Escolhe qualquer número de três algarismos distintos, por exemplo, 875.

Escreve este número de trás para frente: 578

Subtrai o maior do menor.
875 - 578 = 297

Agora inverte também esse resultado (792) e soma as duas parcelas.

297 + 792 = 1089   => O Número Mágico!!!!

Experimenta!!

 

MATRIZES

OBS. Não foi possível incluir o símbolo de "Matrizes" devido a limitações do Blog.

Chamamos de matriz m × n a tabela de números reais com m linhas e n colunas.

Exemplos

I. Matriz quadrada (m = n)

1   2

        (matriz 2 x 2)

2  4

II. Matriz retangular (m ¹ n)

5   3

 (matriz 3 x 2)

4   8

5   9

III. Matriz linha (m = 1)

(1, 5, 6, 8) (matriz 1 × 4)

IV. Matriz coluna (n = 1)

   6

   8       (matriz 3 x 1)

  10

Podemos dizer que aij – elemento da i-ésima linha e j-ésima coluna

                a11   a12   ...   a1n

Am x n =    

                a21   a22   ...   a2n

                am1   am2   ... amn

Algumas observações:

A matriz quadrada com m linhas e n colunas é chamada de matriz de ordem n.

Chamamos de diagonal principal da matriz quadrada ao vetor formado peloscelementos aij onde i = j

TIPOS DE MATRIZES

Matriz Diagonal

É a matriz quadrada, tal que aij = 0, para i ¹ j

Exemplo

  1  2

  

  2  4

Matriz Nula

Todos os seus elementos são iguais a zero.

Exemplo

0  0 0

0  0 0

0  0 0

Matriz Identidade

É a matriz quadrada de ordem n tal que todos os elementos da diagonal principal sejam iguais a 1, e os demais sejam iguais a zero.

Exemplo

       

            0  0  1

            

   I3 =   0  1  0

          

            1  0  0

OPERAÇÕES COM MATRIZES

I. Soma / Diferença de Matrizes

Chamamos de soma / diferença de duas ou mais matrizes A e B, à matriz cujos elementos são a soma dos elementos de A e B. Para haver soma ou subtração, as matrizes devem ser iguais.

Exemplo

         1   2   3             8   7   6           9   9   9 

A =    4   5   6      +     5   4   3     =    9   9   9

         7   8   9             2   1   0            9   9   9 

II. Produto de uma matriz por outra matriz

Sejam as matrizes A = (aij) m × n e B = (bij) m × n, onde, para que seja possível a multiplicação entre as matrizes A e B, o número de colunas de A deve ser igual ao número de linhas de B _ n1º = m2º. O produto AB é a matriz C = (cij)m × n 

Cij = aijbij + ai2b2j + ai3b3j +...

Exemplo

                

               a11   a12                         b11   b12   b13

A2 x 2 =                       B2 x 3 = 

               a21    a22                        b21   b22   b23

                a11b11 + a12b21   a11b12 + a12b22   a11b13 + a12b23    

A x B = 

                a21b11 + a22b21   a21b12 + a22b22   a21b13 + a22b23

COMUNICADO

Caros leitores,

Bom dia!

Venho, através deste, pedir desculpas pelo período sem novos posts. Estive afastada devido a problemas de saúde; no entanto, a partir de agora, procurarei seguir a agenda do blog conforme o fazia anteriormente.

Abraços e bons estudos.

Professora Danielle Cavalcante Soares.

VÍDEO AULA - Sistemas de Numeração

SISTEMAS DE NUMERAÇÃO - Conceitos Iniciais

Se hoje é sábado em qual dia da semana estaremos daqui a 237 dias ? 

Se estamos no mês de julho, em qual mês estaremos daqui a 38 meses ? 

Perguntas deste tipo são muito pertinentes com o primeiro tema que iremos discutir nesse caderno, no caso os sistemas de numeração. A forma de organizar as " coisas " em lotes de 10, lotes de 7, ou ainda, lotes de 12, mostra como o ser humano procurou agrupar os elementos de um determinado conjunto ao longo história. Vamos começar a introduzir essa ideia, navegando pelos sistemas de numeração.. O conceito de número, com o qual estamos tão familiarizados evoluiu de modo muito lento, até os dias de hoje. Mas a relação que o homem primitivo e o moderno guardam com o número é diferente: para o primeiro, o número era um ente ligado à natureza e seus fatos, para o segundo, o número é uma conquista do pensamento abstrato. Por sua vez, o processo de contagem surge nos povos primitivos: a necessidade do registro do número de ovelhas, porcos, cabras etc. que pertenciam a uma aldeia. O número de dias entre uma estação climática e outra, e assim por diante. Nos períodos mais primordiais da contagem, fazia-se uso dos dedos das mãos e pés para associar o número de objetos de uma dada natureza e os objetos em si. Entretanto, para a contagem de grandes números, esse método era de pouca eficiência, e havia a necessidade da elaboração de um método melhor para contagem, sistematizando-o de alguma maneira. Bases Numéricas e Teorema Fundamental da Numeração Nesta filosofia, surgiram as primeiras bases numéricas. As bases numéricas consistem de um conjunto finito de algarismos com os quais podem-se representar qualquer outro número. Qualquer número é algum tipo de representação nesta base. O sistema atual de base 10 consiste em 10 algarismos, a saber: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Ele é tão difundido que poucas vezes nos questionamos 3 sobre ele: o número 536 é uma combinação, o 5 representando a quinta centena, o 3 a terceira dezena e 6 unidades. Mas, este mesmo número é expresso de modo totalmente diferente num outro sistema de base não decimal. Tendo sido escolhido o conjunto de símbolos básicos, os sistemas de numeração têm por regra formar os demais números por algum tipo de repetição dos algarismos básicos e pela soma dos valores. Assim eram os sistemas egípcio, grego e romano. Por volta de 3500 aC, os egípcios usavam figuras para representar seus numerais. O sistema que eles utilizavam consistia em separar os objetos em grupos de 10, mas não tinham um símbolo para o 0 (zero). Os números eram formados pela justaposição desses símbolos, os quais podiam ser escritos em qualquer ordem: a posição do símbolo não alterava o seu valor. Esses sistemas de notação apresentavam um grande inconveniente: à medida que números maiores são necessários, estes exigiam um número excessivo de algarismos para representá-los, e, além disso, operações numéricas nestas representações eram longe de serem óbvias. Tais dificuldades foram superadas pelos babilônios, quando então eles atribuíram importância à posição relativa dos algarismos na representação do número. Os babilônios usavam base 60 (isto é, 60 algarismos) e seus símbolos eram combinações de cunhas verticais. Atualmente, quase todos os povos usam o sistema de numeração decimal, e os mesmos algoritmos básicos da aritmética. Este sistema é o sistema hindu-arábico e foi introduzido pelos indianos e difundido pelos árabes através da Europa. Esse sistema usa dez algarismos, e é posicional: cada mudança à esquerda é equivalente a multiplicar por 10. 

VÍDEO AULA - Proporção